|
The Scandal of Geometry The circle is an idealized object, the fundamental ultimate in perfection. In Euclidís geometry, the circle is the only geometrical area that appears in a fundamental postulate. Euclid constructed his geometry based on five postulates. Four of Euclidís five basic postulates seem trivial enough to be considered as axioms. However, the fifth one, the parallel postulate, from the very beginning was considered as insufficiently plausible to qualify as an unproved assumption by mathematicians. For two thousand years, mathematicians unsuccessfully tried to derive it from the other four postulates, or to replace it with another more self-evident one. Euclid himself did not quite trust this postulate. He postponed using it in a proof for as long as possible, until his 29th proposition. A modified version of this postulate (equivalent to the original one) is as follows: For every line l
and for every point p that does not lie on l
To make Euclidís geometry rigorous, many larger systems of axioms have been proposed. The one proposed by David Hilbert was not the first, but was the closest in spirit to Euclidís. Today, a system of geometry without a form of the parallel postulate is called the neutral geometry. The discovery of non-Euclidean geometry occurred in the nineteenth century with the works of János Bolyai and N. I. Lobachevsky. (There is evidence that Gauss also discovered some of the non-Euclidean results, but did not publish them.) One of the most prominent non-Euclidean geometries is Hyperbolic geometry, which comes from the neutral geometry combined with the Hyperbolic Postulate: For every line l
and point p not on l there exist at least two
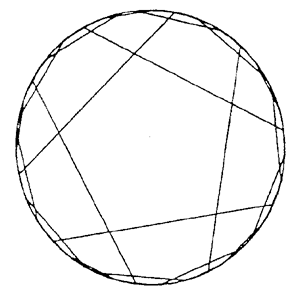
We can prove, in this geometry, that the sum of the angles of any triangle is strictly less than 180o (p). Interestingly, a direct relationship between hyperbolic geometry and Einsteinís special theory of relativity was discovered by the physicist Arnold Sommerfeld in 1909, and elucidated by the geometer Vladimir Varichak in 1912. Since a starís gravity bends light toward itself, a triangle formed by light rays between three stars has this geometry (Figure 7). So, in some ways, this non-Euclidean geometry is a better description of the real interstellar universe than our traditional Euclidean geometry.
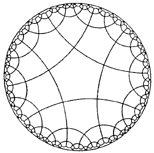
Figure 7. Light rays bend between stars, as do lines in hyperbolic geometry. To explore hyperbolic geometry, Eugenio Beltrami constructed an explicit model in 1866. This model, now known as the Klein model, represents n-dimensional hyperbolic space by an open ball in Euclidean space, and represents hyperbolic lines by Euclidean straight-line segments in the ball (Figure 8).
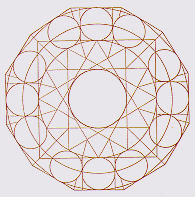
Figure 8. The Klein model of tiling in hyperbolic space with Euclidean straight lines. Another model was invented by Poincaré. His geometric model is conformal, which means it preserves angles. The two-dimensional model maps the hyperbolic plane of all space onto a unit-radius size disk. Here, hyperbolic lines are represented by arcs of circles perpendicular to the bounding circle of the unit disk. As everything in this model is inside the unit disk, its circumference represents infinity, and outside the boundary circle there is absolutely nothing. To understand the Poincaré model, consider that you are in the center of such a circular world, and want to walk away toward the boundary circle at infinity. From your local perspective, each step you take is the same size. But from the point of view of an observer outside this plane, the first step is followed by successively smaller steps. Your steps get progressively smaller, to the observerís eye, by the ratio of (1-r2)/2, where r is your distance from the origin in this model [9]. Let us see what we can do in this circular world that we cannot do in our world of apparently Euclidean geometry. Consider that we want to cover a Euclidean surface with some simple type of regular polygon, without any gaps or overlaps. We see that an equilateral triangle can cover a surface, as can a square, or a regular hexagon. But no other regular polygons can do this. The reason is that if p is the number of sides of a regular polygon (call it a p-gon), and q is the number of p-gons around a vertex, then the interior angle of each p-gon is (p-2)p/p, and around each vertex we have the sum of angles q(p-2)p/p = 2p to make a circle. This reduces to (p-2)(q-2) = 4. Thus, for the 3-gon (triangle) we have q = 6, for the 4-gon q = 4, for the 6-gon q = 3, and no other regular polygon covers a surface by itself. However, this is not the case in the hyperbolic plane. Here, the sum of the angles of a triangle is always less than p. Following the same analysis, this makes (p-2)(q-2) > 4. So we are able to cover a hyperbolic plane by other regular p-gons such as pentagons (Figure 9). Here, we have four regular pentagons fitting exactly around each vertex in this non-Euclidean space.
Figure 9. Tiling of a hyperbolic plane by pentagons with regular angles. The relationships between Euclidean and hyperbolic geometries can be seen by comparing two images that treat a single theme using these geometries. This could be seen in two patterns of fall leaves, shown in Figures 10 and 11. It can also be seen by comparing two similar works by M. C. Escher, showing alternating angels and devils [10]. The Euclidean pattern is just a piece of the whole, which could be extended infinitely (Figure 10). In contrast, the non-Euclidean pattern presents the entire world of angels and devils, bounded by a circle (Figure 11).
Figure
10. Fall Leaves, by Jill Ethridge. Another example of Euclidean
tessellation is Escherís Angel-Devil Symmetry Drawing E 45, from
1941, on the Euclidean plane [10].
Figure
11. Hyperbolic Fall Leaves, by Douglas Dunham (published with the
kind permition of the author). Another example of
hyperbolic tessellation is Escherís non-Euclidean Angel-Devil pattern from
1960, Circle Limit IV, that fills the unit circle to infinity, covering
the entire hyperbolic plane [10, 10a].
Earth and Heaven In Aristotleís Metaphysics, Eudoxusís astronomy is described with circles and spheres [11]
Eudoxus supposed that the motion of the sun or of the moon involves,
The geometrical descriptions of the astronomical heavens were paralleled six centuries later by Plotinus, in a very mystical discussion of where souls go [12].
There is, we may put it, something that is center; about it, a circle of
light
This view of heaven and earth in terms
of circles is evident in the construction of the great Roman temple to
the gods and the planets, the Pantheon [13a].
Its dome exactly contains a sphere, with an open circle on top to communicate
with heaven and provide light (Figure 12).
Figure
12. Interior of the Pantheon, in Rome. The light comes from a circular
Almost in an echo of the eastern philosophy of the wheel of fate and life, Shakespeare uses the circle to indicate the recurrence of circumstances, or fate. The bastard Edmund recognizes that his amoral victories have only brought him back down to nothing in the final scene of King Lear [14]. The gods are just, and of our pleasant vices Make instruments to scourge us. The dark and vicious place where thee he got Cost him his eyes. Edmund: Th' hast spoken right; 'tis true. The wheel is come full circle; I am here. Virtues associated with the circle include
the thirteenth-century construction in Winchester, England, of King
Arthurís Round Table, now mounted on the wall of the Great Hall. This
was taken as a symbol both of the sacred and of knightly equality under
God [15]. The design and appearance are circular
for both the main part and the tower of St. Sepulchreís church, in Cambridge,
England (c. 1130) [16a]. The circle has been
used not only by the men of the church, but also by women, such as by the
religious visionary, abbess, composer, artist, and medieval medic Hildegard
von Bingen (1098-1179) (Figure 13) [16b].
Figure 13. A circular mandala created by Hildegard von Bingen in the 12th century. The circle is also the basis for the
intricate "rose" window patterns, such as those seen on three of the faces
of the gothic Cathedral of Chartres, France (Figure 14) [17].
Other famous rose windows include those of Sainte Chapelle and of Notre
Dame in Paris (Figures 15, 16).
Figure
14. The north, west, and south rose windows on the cathedral
Figure
15. The rose window on the Sainte Chapelle of Paris.
Figure 16. The rose window on the west of the Notre-Dame of Paris, from the 13th century. The New Jerusalem pattern is
a circle surrounded by twelve smaller ones (in the ratio of the earth to
the moon), arranged in a pattern like the numbers on a clock face (Figure
17). The twelve circles are grouped in threes, with a dodecahedron circumscribed
tangent to them [15b]. The number twelve has been
seen as a desirable divisor for circles since Babylonian times. It is worth
noting that this is exactly double the number that is mathematically required
for the symmetric version of this goal, described below.
Figure
17. The New Jerusalem pattern of twelve circles around one.
|