|
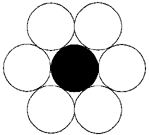
The Kissing Number An interesting measure of the size of
a circle is the possible number of neighboring circles. One can place circles
in a rectangular grid, with identical circles touching above, below, to
the left, and to the right of the central circle. However, a tighter arrangement
can be made, with hexagonal symmetry. Here, each circle is surrounded by
six equivalent ones. This arrangement has the special property that all
the neighbors are touching two other circles off the original one. In other
words, six circles will exactly surround one, in two dimensions. Items
forced on to a flat surface, if short on space, will get six neighbors,
and tend to take on the shapes of hexagons themselves, as in a honeycomb
(Figure 18).
Figure
18. A circle encircled by six circles shows
Another example of the kissing number
in a plane is carbon atoms in graphite, as in pencil "lead" (Figure 19).
Here, layers are made of carbon atoms forming three bonds in the plane
to similar atoms. The atoms form flat hexagonal rings, which are surrounded
by identical hexagons.
Figure 19. Carbon atoms in two dimensions form hexagonal sheets, called graphite. While carbon in the graphite form is
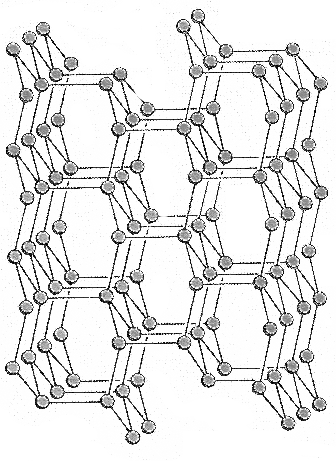
essentially a two-dimensional structure, the diamond form of carbon is
a covalent network solid, extending equally in three dimensions (Figure
20).
Figure 20. Carbon atoms in diamond extend through three dimensions.
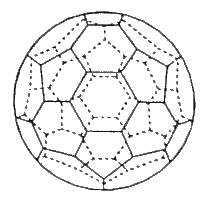
In the last few years, a third fundamental
form of the element carbon has been discovered, in which individual atomic
bonds are made in two dimensions, but the overall shape obtained is three
dimensional. Specifically, a group of 60 carbon atoms will wrap itself
into a sphere (changing some hexagons into pentagons). This forms a compound
called buckminsterfullerene, or a buckyball (Figure 21). This is
named after the inventor of the similarly shaped geodesic dome, Buckminster
Fuller.
Figure
21. A buckyball, or buckminsterfullerene, the spherical C60
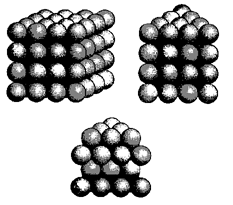
The problem of stacking or packing balls efficiently has been an interesting puzzle for four centuries. While people have stacked things for millennia, it was in 1611 that Kepler posed the Sphere-Packing Problem [19]. What kind of stacking of spheres can be proven to be the densest possible? A first layer of spheres can be arranged
in the rectangular or hexagonal patterns of circles in a plane, described
above. Such layers can be stacked exactly atop one another, yielding respectively
the arrangements called the body-centered (or 3-dimensional) cubic lattice,
and the face-centered cubic lattice or cubic close-packed form (Figure
22). However, if flat layers are stacked repeatedly in a staggered way,
a third, most dense pattern emerges, called the hexagonal lattice, or hexagonal
close-packed [20].
Figure
22. Oranges or atoms in three dimensions
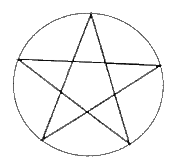
All three of these packings are found in nature, as are mixtures of these with less regular forms. Interestingly, elemental metals use all forms, in patterns that do not always correlate with electronic symmetry. For example, potassium, chromium and tungsten prefer the body-centered cubic form, as does iron at room temperature. However, iron at other temperatures takes on the cubic close-packed form, as do copper, silver, and gold. In contrast, the elements in the same period directly below iron (i.e., ruthenium and osmium) prefer the hexagonal close-packed arrangement, as do most of the rare-earth elements, as well as zinc and titanium [20]. The number of circles that can surround a circle in any given dimension is called the "kissing number" by mathematicians. On a one-dimensional line, this is two (left and right). In a two-dimensional plane, as we discussed, the kissing number is six (see Figure 18). The kissing number is 12 in three dimensions, as in the above hexagonal close-packed arrangement (with six in the plane, three more above, and three others below). In theory, a four-dimensional sphere should have a kissing number of 24, in eight dimensions it is 240, and in 24-dimensional space the kissing number is 196,560 circles touching the center circle at once [19]. The kissing number of six for a circle means that it is possible to construct a regular hexagon (and consequently a six-pointed star) by using the radius to cut the circle into six equal arcs. Unlike the simplicity of the construction of a six-pointed star, it is a challenge to use only a compass and straight edge to construct a pentagram, a five-pointed star extending from a regular pentagon. To do this task, we need to know how to find the "Golden Mean" of a line segment. The Golden Mean is a cut in a line segment such that the ratio of the larger section to the smaller one is the same as the ratio of the entire line segment to the larger one. It is possible to find the Golden Mean of a given line segment using a compass and straight edge. The Golden Mean has been used extensively in art and architecture from the ancient times of the Egyptians and Greeks up to today. The larger section of the Golden Mean of the radius of any circle divides the circle into ten equal arcs, which enables us to construct the pentagram [21]. The complexity of these procedures, or the harmony and order of the completed form, created the association of mysticism with the combination of a pentagram inscribed in a circle, the chosen symbol of the order of the Pythagoreans, sometimes associated in western tradition with witchcraft (Figure 23).
Figure
23. The pentagram of the Pythagoreans.
Poetry of the Whirling Dervishes The word Sama means the joyous but ceremonial religious excitement of the Sufi faithful, either individually or together. Today, it also is any of the famous whirling and circling dances done to the lamenting reed pipe and the pacing drum, performed by the Mevlevi dervishes. These are the disciples of the Sufi poet and spiritual leader, Jalal al-Din Molavi al-Rumi (1207-1273). Rumi is, by one account, the best-selling poet in the United States today [22]. Rumi is one of the most well-known of the historical Persian-language poets, and his mystical poems have been sung from Afghanistan and India to Iran and Turkey for seven centuries. He feels a transcendent, romantic relationship and obsession with the creator, and equally with all of creation. He was born in Balkh (now in Afghanistan). The Mongol invasions caused his family to flee, while he was still a child, to Konya (now part of Turkey), where he lived and died. Rumi was a theologian, preacher and conventional religious scholar through age 37. Then a man in his sixties arrived, a wandering dervish of wild demeanor named Shams al-Din, who transformed Rumiís world view, despite resistance from Rumiís many conventional religious pupils. Rumiís new ecstasy with the world led him to express his feelings with poetry and with a revision and popularization of the whirling dances of the dervishes. He would even dance and sing to the sounds of the metalworkers in the bazaar. The Sama, in the mystical culture of Persia popularized by Rumi, is demonstrated by a person under the influence of a deep, internal feeling of excitement and love for the spiritual beauty of creation. The person stands up, without feeling self-conscious, and starts circling and whirling. This is especially done according to certain conventions of hand positions and other dance movements that symbolize the spiritual attitude of the obsession with love of the universe. To this day, this is performed in Turkey every year for thousands of visitors, during the week around December 17, the anniversary of Rumiís death. The Mevlevi dervishes consider the space
in the house of the Sama to represent a spherical form of the universe.
An imaginary axis divides it into western and eastern pieces. At the center
is a small circle, called the "pole." After music and singing to candle-light,
the circle dancing is done as shown (Figures 24 and 25). The hands are
open and arms extended. The right palm faces up to the spiritual sources
of heaven, while the left palm faces down to the world, with the dervishís
heart in between, as a medium or bridge. The left foot is fixed, while
the right foot causes the body to circle.
Figure
24. The religious devotional activity of the "whirling dervish"
bring into dancing the souls of the Sufis. Sun, moon, and stars dancing around the circle, we dancing in the midst ó set that midst a-dancing. Your grace minstrelwise with the smallest melody brings into the wheel the Sufi of heaven. circles around God like a mill. My soul, circumambulate around such a Kaaba; beggar, circle about such a table. widening rings of being. of birds flying, each particle circulating on its own. Is the one I love everywhere? I am what I am. Your actions in my head, my head here in my hands with something circling inside. I have no name for what circles so perfectly.
|