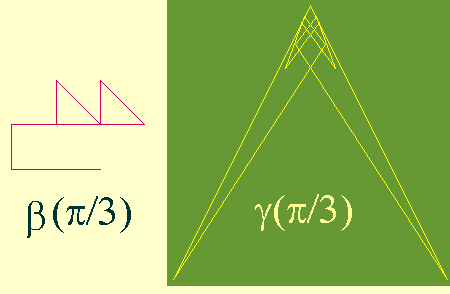4. ConclusionThere are many open questions as well as the directions of further research. First of all, it can be noted that all Brownian walk graphs have certain "direction" of evolution, even in the case of transcendental numbers (with non periodic continued fraction expansions). This means that numbers from the same class of equivalence of the relation "=mod 8" are predominant in the particular expansion. On the contrary, having the "portrait" of a certain number will reveal what class of numbers is dominant in the continued fraction expansion. Second, it should be examined what mapping f is to be applied on x so that b(f(x)) is some elementary transformation of b(x), like translation or rotation, etc. Finally, what information can be extractes from the shape of b(x) if x is a transcendent number? For example, what is its fractal dimension, assuming the length m is big enough? A similar question concerning fractal dimension can be stated for symmetrograms. AppendixOur examples are created with the program system Mathematica. Two fragments of programs we used are given here. The first fragment corresponds to the Algorithm A. As it can be seen, it uses the built-in package Number Theory which includes a software for continued fraction expansion of a given number.
The second fragment is, in fact, Algorithm B. Note that the first line of the above's fragment should be also inserted as the first line if the program runs separately.
These programs are called by brown[x, m] i.e. by symm[x, m], where x is the number which "portrait" is to be made. Thus, running the lines brown[Pi/3, 15]; symm[Pi/3, 12]; Mathematica 3.0 will produce two figures that are shown below. These are b(p/3) in 15 points and g(p/3) in 12 points.
|