Algorithm A.
1. Take the
continued fraction expansion of x as above. Cut
the sequence {ak}
up to the (m+1)-th term so to obtain a0,
a1 , ... , am
;
2. Replace
ai by a'i
= ai (mod
8); In this way, the number x is represented by a'0
,
a'1 , ... ,
a'm where a'iÎ{0,1,
...,7} .
We will write a(x) = (a'0 ,
a'1 , ... , a'm
);
3. Starting
by the point (x0 , y0) = (0, 0) create
a sequence of points in R2, {(xk , yk),
k = 1,2, ...,m+1} following the rule xk+1 = xk+
p, yk+1 = yk+ q, where p and q depend
on a'i as it is shown in the table:
| a'i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
| p |
1 |
1 |
0 |
-1 |
-1 |
-1 |
0 |
1 |
| q |
0 |
1 |
1 |
1 |
0 |
-1 |
-1 |
-1 |
4. Draw the polygonal line
b (x)
= {(x0 , y0),
(x1, y1), (x2, y2),
... , (xm+1, ym+1)}.
Note that the the table encodes the direction of the trajectory of a
moving particle according to the compass rose : E, NE, N, NW, W, SW, S
and SE. This pseudorandom Brownian walk was used by the
authors of [1] to investigate the quantity
of information being hidden into the DNA molecule chain.
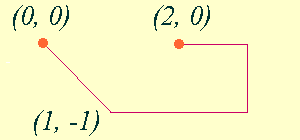
Let us try this algorithm on a simple example. Take the fraction x
= 61 / 117. Its continued fraction expansion is 61/117 = [0, 1, 1, 11, 5], so, m =
4. Applying the second stage on the sequence 0, 1, 1, 11, 5 will result
in "mod 8" reduction to 0, 1, 1, 3, 5. The polygonal
line defined by 6 vertices (0, 0), (1,-1), (2,-1), (3,-1), (3, 0),
(2, 0) is a result of applying the third stage. In this way we obtain the
following "portrait" of the number
x:
Quadratic irrationalities
The Euler-Lagrange theorem claims that a continued fraction expansion of
x
is periodic, if and only if x is
irrational of quadratic type. This means that x is
a solution of the quadratic equation x2 + p x + q =
0, with p, q ÎR.
The next figure shows the graphical outputs obtained by Algorithm A, for
the numbers x1 =
(35 + 3 Ö205)/62,
x2= (831+31Ö957)/626
and
x3 =
(7
+ Ö2117)/44.
The corresponding continued fractions are x1
=[á1,3,1,7ñ],
x2 = [
á2,1, 6, 8,1,4ñ]
and x3 =
[á1, 4, 1, 7,1ñ].
Metallic means family
Maybe the best known continued fraction
expansion is f =
[1, 1, 1, 1, ...] = (1+Ö5)/2 -
the famous Golden Mean number, alias the positive solutions of quadratic
equations x2 - x - 1 = 0. It is easy to see that
Algorithm A, applied to f
will produce a horizontal line. But there exist an interesting family of
numbers that generalizes the Golden Mean number. This is so called Metallic
Means Family (MMF) defined as the positive solution of quadratic
equation x2 - px - q = 0 (p, q
are natural numbers), i.e.
s(p, q)
= (p+ (p2+4q)1/2)/2.
In special cases, we have [3, 4]
the Golden Mean s(1,
1), the Silver Mean s(2,
1), the Bronze Mean s(3,
1), etc. But these
"noble" metal means are not very
creative from the point of view of Brownian graphs, because all of them
are of the form [p,ápñ] and
therefore yield
straight lines. But many of them are real "artists". For example,
s(3,3)=(3+Ö21)/2,s(1,
8) = (1+ Ö33)/2,
s(1,
32) = (1+ Ö129)/2
and s(1,
578) = (1+ 3Ö257)/2
creates nice Brownian friezes that are shown below.
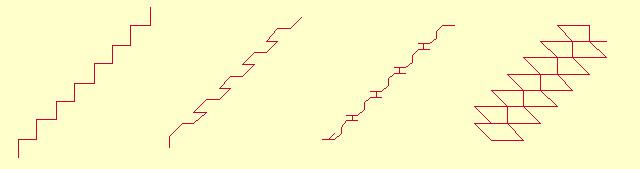
E - friezes
An important part of the set of irrational numbers is the set of
transcendental numbers. These numbers fail to be roots of any algebraic
polynomial equation with real coefficients and their continued fraction
expansion is non periodic.
We will start with the number e = 2.71828182845905...
- the basis of natural logarithms. It has the continued fraction expansion
e = [2,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,1,14,1,1,...] .
Note that, starting from the
third term, the pattern {2n, 1, 1}, n = 1, 2, 3,
... repeats endlessly. Obviously, the "mod 8" operation will
transform this pattern into {{2n mod 8}, 1, 1}, n
= 1, 2, 3, .... In this way, a non periodic expansion becomes
periodic, i.e. we will have
b(e)
= (2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 0, 1, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1,
0, ...) ,
where the number "1" appears twice as frequently as the other numbers.
This will make the "portrait" b(e)
a horizontal frieze. What is peculiar
is that the same property, to produce horizontal friezes, remains if we
perform some simple operations over
e. The next figure shows b(e),
b(e1/3)
(with m = 60), b(e2)
(with m = 100) and b(e/3)
(with m = 130).
Other transcendental numbers
Finally
we want to examine some other transcendental numbers, like
p, Log(p),
or Euler gamma g
» 0.577216..., for example. The
figure below shows b(p), b(Log(p))
and
b(g) for m = 80
points. Note that no rules or patterns are visible on these
graphs and therefore they really looks like Brownian walk paths.
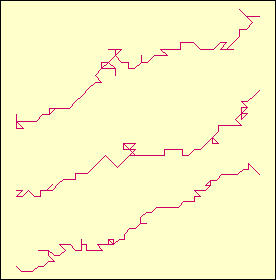
The following figure looks similar as the previous one although the
numbers shown are not transcendental but irrational. The graph on the top
corresponds to the number t = Ö2
+ Ö3 which is the greatest solution of
the biquadratic equation t4 - 10 t2
+ 1 = 0. The middle graph is b(
5 1/3 ) while the last one is b(
7 1/5 ).

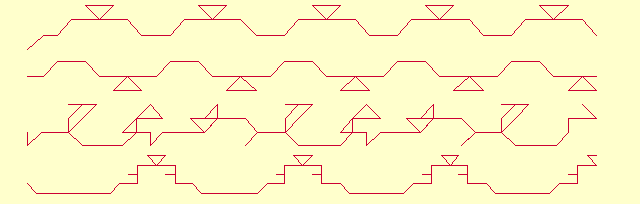
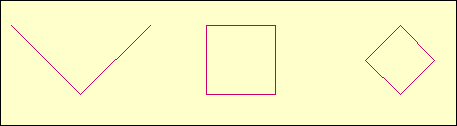
Hyperbolic functions are composed of exponential ones. Therefore, they
also can produce periodic sequences
a(x) that causes periodic graphical
outputs that sometimes may look like simple geometric shapes. Displayed
below are "portraits" of Tanh(0.5), Coth(1) and
Coth(-1).
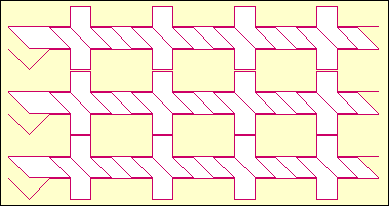
Trigonometric functions are supposed to be a reach source of transcendental
numbers. The next figure shows
"Brownian paths" made by tangent function. It is composed out of three
rows. Each row is made by
drawing graphs b(Tan(1/2)), b(Tan(1/3))
and b( Tan(1)) put side by
side.
The inverse problem
Can we find a number that corresponds to a certain plane figure being drawn
as a union of eight types
of segments: {(0,0),(1,0)} - having code "1", {(0,0),(1,1)} -
code "2", {(0,0),(0,1)} - "3",
{(0,0),(-1,1)} - "4", {(0,0),(-1,0)}- "5", {(0,0),(-1,-1)} - "6",
{(0,0),(0,-1)} - "7", {(0,0),(1,-1)} - having code "0" or "8"?
The answer is "yes" if the figure is finite (bounded) or infinite (unbounded)
but
periodic. If these requirements are not fulfilled, then it is a composition
of two or more finite or periodic
graphs. If the figure is finite, the solution is trivial. If it is
periodic, given by repeating the period a0 , a1,
a2, ...,
ak, then the corresponding number
x is the biggest solution of quadratic equation
x = [á a0,
a1, a2,
...,
ak,
xñ].
If the figure is composed of one finite and one periodic part, where
the first is given by a0
,
a1, ..., an
while the periodic part is given by a0,
a1, ..., ak,
then the
corresponding number is y = [a0, a1, ...,
an,
x], where
x is given by the same equation as above.
Example. The "3D staircase" figure
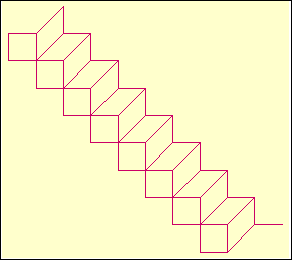
can be drawn by repeating the motif
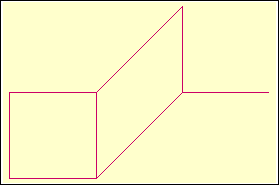
that is encoded by the sequence 7, 3, 6, 7, 3, 5, 7,
1, 2, 1. The number that will cause an infinite repeating of this motif
is given by the infinite continued fraction x = [á7,
3, 6, 7, 3, 5, 7, 1, 2, 1 ñ].
It is therefore the biggest solution of the quadratic equation x
= [á7, 3, 6, 7, 3, 5, 7, 1, 2, 1, x
ñ], i.e.
the number as strange as x=(474047+Ö337648155621)/144218.
NEXT
VisMath Home