|
Tait series
In the knot theory Borromean rings are the foremost examples having with
two remarkable properties: three mutually disjoint simple closed curves form a
link, yet no two curves are linked, and if any one curve is cut, the other
two are free to separate. In the case of 3-component links those two properties
are inseparable: one follows from the other. In the case of n-component links
(n>3), n-Borromean links could be defined as
n-component nontrivial links such that any two components form a trivial link.
Among them, those with at least one nontrivial sublink, for which we will keep
the name "Borromean links", will be distinguished from the Brunnian
links in which every sublink is trivial [8].
It seams surprising that besides the Borromean rings, represented by the
link 623 in Rolfsen notation, no other link with
the properties mentioned above can be found in link tables
[9,10].
The reason for this is very simple: all existing knot tables contain
just the links with at the most 9 crossings. In fact, an infinite number
of Borromean or Brunnian links exist, and they can be derived as infinite series.
The first such series of 3-component links, beginning with the Borromean rings,
was discovered by P.G.Tait [11].
Their geometrical source is easy to recognize:
the limit case for n=1 yields the regular octahedron {3,4}, while the
series of (3n)-gonal antiprisms are obtained for n>1.
Alternating their corresponding projections (well known in geometry as Schlegel
diagrams) provides the series of achiral 3-Borromean links. 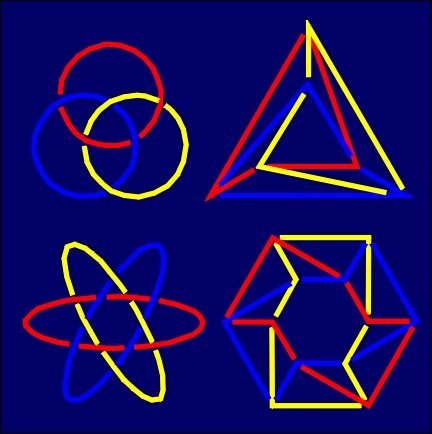
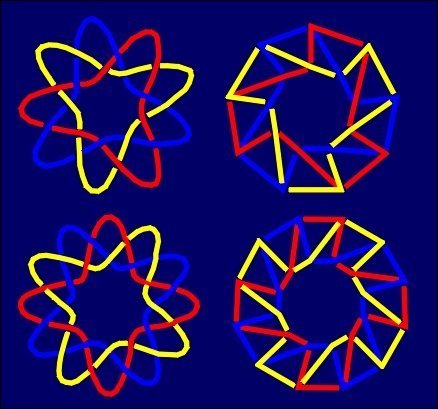
|