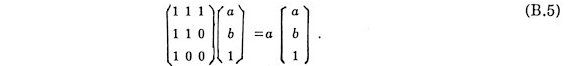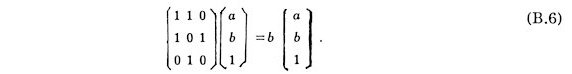Appendix 

Appendix A 
On the Similarity factor t^-3

An interpretation is given on the fact that the similarity factor t^-3 is the minimum value for three dimensional Penrose tiling with icosahedral symmetry and self-similarity. Six quasibases are a, b, g, x, h, z introduced in Chapter 2. The vectors that can be expressed as a summation of these vectors are restricted as follows. 

Along a 5-fold axis (parallel to a), it is in the form 

and the length is 

Along a 2-fold axis (g + z ) 

whose length is 

Along a 3-fold axis (x + h + z ) 

whose length is 

In Table 10, the ratio of distance to the corresponding minimum value are given for some small values of (m, n). The ratios 5t and t can not be realized for 3-fold axis. On contrary, the ratio t³ can be realized for all symmetry axes as shown in the last column in Table 10. In order to expand an O₆, therefore, the value is the first candidate of the similarity factor from numerical point of view. As a matter of fact, the suitable arrangement is actually found as shown in Chapter 2. 
 

Table 10 The possible length along symmetry axis and the ratio to the corresponding minimum value 
 
 

Appendix B 
Similar Numbers to Golden Number 

Let the lengths of two kinds of diagonals of a regular heptagon be a and b where a>b. They are given by 

where q = p/7. They are respectively the biggest root of cubic equations 

and satisfy the following relations 

and 

It is noted that the relations are natural extension of that for a regular pentagon 

Two sequences 

and 

associate with them as Fibonacci sequence does with regular pentagon. Similar relations hold generally for the lengths of diagonals of regular polygons. The matrices can be regarded as those for one-dimensional wave propagation.