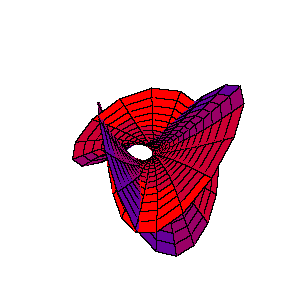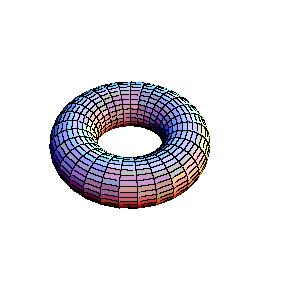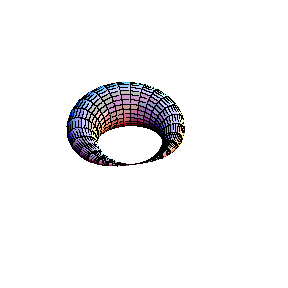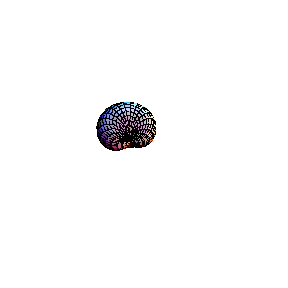Visualization
of simple Aleksandar T. Lipkovski
1 IntroductionIn the first elementary study of complex plane algebraic curves, appearance of the real part of the curve may be misleading for students who begin to study the subject. A proper picture, however, should be viewed in four dimensional space. This is possible in few ways. Time can be used as the fourth coordinate and the object represented in motion. The other possibility is to use colouring or shading and represent the object as a coloured or shaded projection in three-space:
In this short note such approach for viewing the topology of the singular point has been used. Animations have been also used to demonstrate the notion of projective equivalence. 2 Plane Cubic SingularitiesA complex plane algebraic curve, defined by the equation f(x,y) = 0 in the complex plane C2, determines two real equations
in R4 and in fact represents a two-dimensional surface in real four-dimensional space. How could this object be visualised in three-dimensional space? Animations based on the projection
will be shown. This projection, naturally, deforms the surface and does not give its real picture. However, the method gives a certain qualitative image of the given complex curve. Using projective classification of third order curves in complex projective plane CP2, i.e. classifying them with respect to group of collineations PGL(2,C), the canonical equation y2 = x3+ax2+bx+c is obtained. The type of the curve depends on multiplicity of the roots of the right-hand-side polinomial. If this polynomial has three different simple roots, it is an elliptic curve. If it has one double and one simple root, the curve is an "alpha" curve with one double point of self-intersection with different tangent lines. Finally, if it has one triple root, it is a "cusp", a curve with one reccurent point. The animations that are shown represent the deformation of the curve y2 = x(x-l)(x-m) when parameters l,m tend to zero, one after another. When first l ® 0, the "alpha" curve with a simple double point y2 = x2(x-m) is obtained. Then, when m ® 0, a curve which has more complicated double point, the "cusp" y2 = x3, is obtained.
y2 = x2(x-m) into the "cusp" y2 = x3 is seen. Colouring of the surface is determined by the fourth (omitted) coordinate Im y, so that self-intersections of differently coloured sheets are actually artifacts created by projecting onto R3.
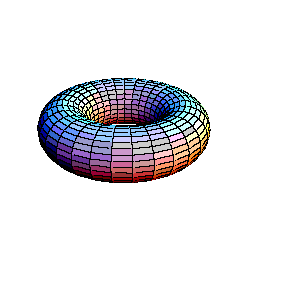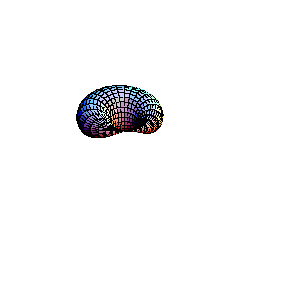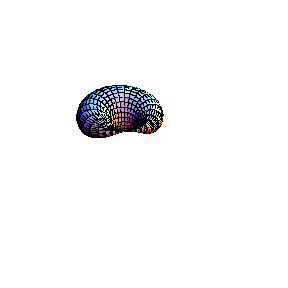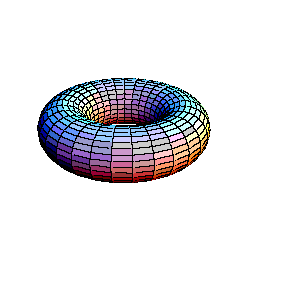
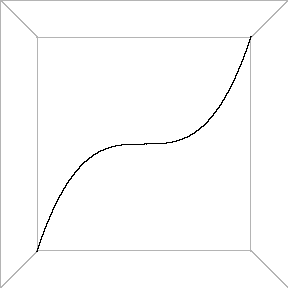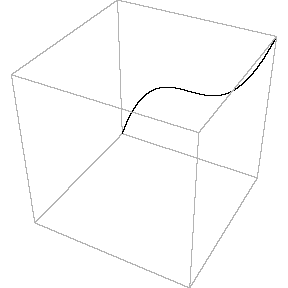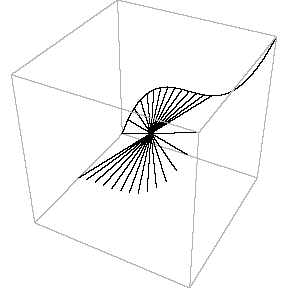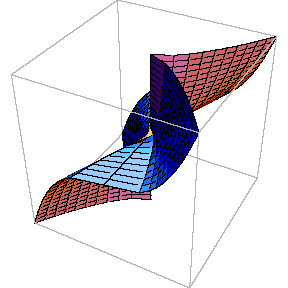
In the second animation a torus is seen. This real surface corresponds to the elliptic curve y2 = x(x-l)(x-m). Then, one of the main circles of the torus contracts into a point, giving the surface of the "alpha" curve y2 = x2(x-m). Topology of the singular point of the "alpha"
curve is clearly visible in this picture: its small
neighbourhood consists of two disks, glued in one point (a
bouquet of two disks). Finally, the inner circle of the
torus collapses to a point , giving the surface which
corresponds to the "cusp" curve Topology of the singular point of the "cusp" type is also visible. Its small neighbourhood consists of a single disk: although badly warped, it is still a topological disk. So, the topological type of the curve is changed: it becomes a sphere.
3 Projective equivalence of cubic and Neil's parabolas
y = x3, and the other one is the semicubic or Neil's1 parabola, or the "cusp" curve y2 = x3. The first mathematician who discovered projective equivalence of these curves was probably Sir Isaac Newton2. In his work on enumeration of third order curves he introduced the first classification of algebraic curves after the ancient conics. Animation shows only a part of the picture which is visible in the real plane R2 or space R3. If the cubic parabola y = x3 in the plane z=1 is drawn, and then a cone over it with vertex in the origin formed, the intersection of that cone and the plane y = 1 is exactly the semicubic parabola z2 = x3. This fact is clearly seen in the animation. 4 LiteratureIf the reader would like to learn more about various facts and ideas mentioned above, further information can be found in the following books. [1] Brieskorn E., Knörrer H., Ebene algebraische Kurven, Birkhäuser, Basel, Boston, Stuttgart, 1981 (English translation: Brieskorn E., Knörrer H., Plane Algebraic Curves, Birkhäuser, Basel Boston Stuttgart, 1986) [2] Griffiths P.A., Introduction to Algebraic Curves, Translations of mathematical monographs 76, American Mathematical Society, Providence, 1989 [3] Griffiths P., Harris J., Principles of algebraic geometry, Wiley-Interscience, New York Chichester Brisbane Toronto, 1978 (Russian translation: Griffits F., Harris Dz., Principy algebraicheskoi geometrii. V 2-h tomah, Mir, Moskva, 1982) [4] Kendig K., Elementary algebraic geometry, GTM , Springer, New York, Heidelberg, Berlin, 1977 [5] Mumford D., Algebraic Geometry. I Complex Projective Varieties, Grundlehren Bd. 221, Springer, Berlin, Heidelberg, New York, 1976 (Russian translation: Mamford D., Algebraicheskaya geometriya. 1. Kompleksnye proektivnye mnogoobraziya, Mir, Moskva, 1979) [6] Reid M., Undergraduate Algebraic Geometry, London Mathematical Society Student Texts 12, Cambridge Univ. Press, Cambridge, 1988 (Russian translation: Rid M., Algebraicheskaya geometriya dlya vseh, Mir, Moskva, 1991) [7] Savelov A.A., Ploskie krivye, Gos. izd. fiz.-mat. lit., Moskva, 1960 [8] Hartshorne R., Algebraic Geometry, Graduate Texts in Mathematics 52, Springer, New York, Heidelberg, Berlin, 1977 (Russian translation: Hartshorn R., Algebraicheskaya geometriya, Mir, Moskva, 1981) [9] Shafarevich I.R., Osnovy algebraicheskoi geometrii, Moskva, Nauka, 1988 (2. ed.) (English translation of the first edition: Shafarevich I.R., Basic algebraic geometry, Grundlehren Bd. 213, Springer, Berlin, Heidelberg, New York, 1974) [10] Walker R.: Algebraic curves, Princeton Univ. Press, Princeton, 1950 (Russian translation: Uoker R., Algebraicheskie krivye, IL, Moskva, 1952) Footnotes:1 William Neil (1637-1670), english mathematician, famous after the rectification of the semicubic parabola (i.e. calculation of its arc length) in 1657.
|