(f) Petrie reports (TPTG p. 86) the measures of the ends of the sarcophagus as:
outer width 38.5 inches (mean); outer height 41.31 inches (mean).
Without doubt the height is intended to be two royal cubits (41.25 inches). The 38.5-inch
outer width is 1 195/225 (1.8666 ...) royal cubits, conveniently equivalent to 52.5 common
cubit digits or 2.1875 common cubits. Compare the latter number with KM 2.1875 inches in
Figure 3. As well, 38.5 inches is equal to 2.2 Roman cubits or 52.8 remen digits: a mile
contains 5280 feet.
The area of the end is thus 3 165/225 (3.7333 ...) square royal cubits.
The quotient of 8 48/225 cubic royal cubits, the contents of the sarcophagus, divided by
2.2 is 3 165/225 (3.7333 ...): again see point (b) above. A further design intention is clear; a
strategy has emerged.
Note that the quotient of the measure 108 8/9 royal cubits, see point (d), divided by
3 165/225 is 29 1/6 (29.1666 ...). The latter number is 14 7/12 (14.58333 ...) multiplied by
two: 14 7/12 inches is the measure of the remen - see Figure 2.
Furthermore, the quotient of 171 1/9 (royal cubits) - also see point (d) - divided by
3 165/225 is 45 10/12 (45.8333 ...) which is 14 7/12 multiplied by 22/7. A clever variant of
this outcome was given architectural form - see point (k) later.
(g) The King's Chamber
The only measure that has been the subject of conjecture in the King's Chamber is the
design intention for the wall height. According to Petrie (TPTG p. 195) the length of the
room is 20 royal cubits (412.24±0.12 inches), the width 10 royal cubits (206.12±0.12 inches).
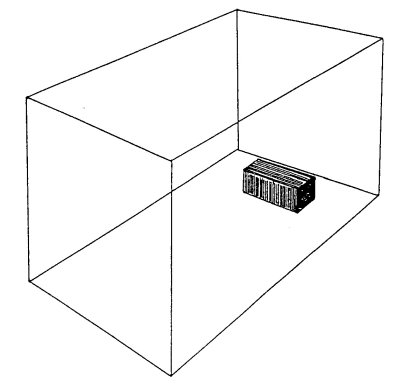 General layout of the King's Chamber (sarcophagus shown)
General layout of the King's Chamber (sarcophagus shown)
Petrie thought the height of 230.09±0.15 inches, that is, 229.94 to 230.24 inches, may
have represented half the diagonal measure of the floor or 11.18 ... royal cubits (230.53
inches if the royal cubit were assigned the traditional value of 20.62 inches, 230.59 inches if
taken at the correct value of 20.625 inches). However, his hypothesis does not fit observed
data. Here is what is going on.
The royal cubit is divided into 28 digit divisions
(Petrie, IM p. 56): cf. the 280 royal
cubit height of the Great Pyramid. Each digit is thus 165/224 inch. Invert this fraction and
multiply by the number of cubic royal cubits in the contents of the sarcophagus:
224/165 × 8 48/225 = 11 169/1125 royal cubits
And 11 169/1125 royal cubits is 229 219/225 (229.97333 ...) inches. The fit is near
perfect. Of additional interest is the fact that 8 48/225 royal cubits is 229 219/225
(229.97333 ...) royal cubit digits. Such remarkable outcomes are worthy of contemplation.
The volume of the chamber is 2230 10/225 (2230.0444 ...) cubic royal cubits
(11 169/1125 × 20 × 10). This is 271 17/33 times the volume of the sarcophagus contents
8 48/225 cubic royal cubits; 271 17/33 is the number 280 divided by 1.03125 which is one-
twentieth of 20.625, the number of inches in a royal cubit.
The area of either the north or the south wall is 223 1/225 (223.00444 ...) square royal
cubits: height 11 169/1125 multiplied by length 20. This area has been inventively used in
the Giza pyramid layout: see the next point.
(h) The Menkaure-Khephren rectangle
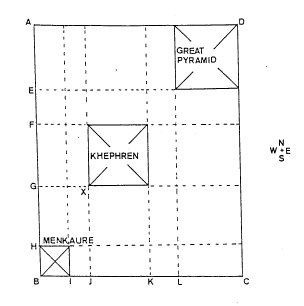 Layout of the Giza pyramids
Layout of the Giza pyramids
In an article entitled A Ground Plan at Giza British researcher J. A. R. Legon utilised
Petrie's measurements of the rectangular area that contains the pyramids of Khufu, Khephren
and Menkaure for a hypothesis on the spacing and sizing of the structures. Of especial
interest in the article is the layout of the Khephren and Menkaure pyramids (GXJB in
diagram), in particular, the north-south distance between the southern sides of the two
pyramids (GB) and the east-west distance between their western sides (GX). The measures
quoted here are from the Legon article; Legon obtained them from Petrie's book The
Pyramids and Temples of Gizeh.
The north-south distance from the southern side of Khephren's Pyramid to the southern
side of Menkaure's Pyramid (GB) is 13,009.7 inches. The east-west distance, the west side
of Menkaure's Pyramid to the west side of Khephren's Pyramid (GX) is 7289.5 inches.
The east-west measure GX, the design intention, is easy to distinguish: it is 353 53/99
(353.5353 ...) royal cubits or 7291 2/3 (7291.666 ...) inches which is equivalent to 500 remen
or 10,000 remen digits of 0.7291666 ... ( 35/48) inch. The accuracy is exceptional, the layout
error a trivial two inches or so. See the measure BU 7.291666 ... inches in
Figure 3.
Return for a moment to the area of the north or the south wall in the King's Chamber:
223 1/225 (223.00444 ...) square royal cubits. Multiply this number by one thousand and an
area of 223,004 4/9 square royal cubits is created. The quotient of this area divided by GX
353 53/99 royal cubits (500 remen) is 630.784 royal cubits or 13,009.92 inches. This is
clearly the north-south distance GB of 13,009.7 inches mentioned above. The accuracy is
stunning: the layout "error" a mere 0.22 inch.
In NADIAE the reasons for the distances between all three pyramids are explicated.
The east-west distance is of further interest: 353 53/99 royal cubits or 500 remen is the
equivalent of 625 Roman feet, the Roman stade. It is also the equivalent of the 600-foot
Greek stade. A Roman foot thus measures (like the "forearm") 11 2/3 inches and a Greek
foot 12 11/72 (12.152777 ...) inches: see
Figures 2 and 5. Zupko (p. 6) records the measures
as [about] 11.65 inches and 12.15 inches respectively. The east-west distance may well be
the first identified appearance of what was later known as the Greek-Roman stade.
Two hundred and sixteen thousand (216,000 = 60 cubed) stades is equal to 1575,000,000
inches or 24,857 21/22 miles, the measure of the world mentioned in the Preamble and
elsewhere.
Of outstanding interest is the fact that ten stades or 72,916 2/3 inches is virtually identical
with the U.S. international nautical mile of 6076.1033 feet or about 72,913 1/4 inches; the
difference is less than 3.5 inches.
(i) The matter of Atlantis
The Greek philosopher Plato who is known to have visited Egypt wrote a colourful
account of a mythical region called Atlantis. A physical description of the place is provided
in his unfinished work Critias. The key interest here is the arrangement and dimensions of
the concentric rings of land (two of them) and water (three of them) that surround the central
feature, an island five stades in diameter which contains, amongst other things, a royal palace
and a Temple of Poseidon.
In total, the circular design is 27 stades in diameter (Lee, p. 152). But now the true value
of the stade is known: 7291 2/3 inches (see point (h)). Here is one of many mathematical
feats concealed by Plato. There are others in NADIAE. One that is memorable is presented
shortly.
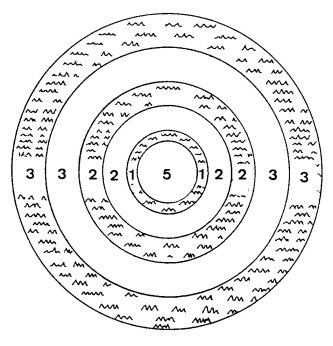 The rings of water and land around the citadel (central island)
The rings of water and land around the citadel (central island)
The circumference of the circular arrangement is 84 6/7 (27 × 22/7) stades or 618,750
inches or 9.765625 miles; 9.765625 is 3.125 squared. Moreover, 9.765625 miles is equal to
(multiply by 3600 - see the Preamble) 35,156.25 common cubits. The latter measure is the
diagonal of a square whose sides are - divide by 99/70 - 24,857 21/22 (24,857.95454 ...)
common cubits. The ancient Egyptian measure of the world is this many miles: see the
Preamble and point (h).
A return to the Great Pyramid is germane.
(j) The height of the King's Chamber was established as 11 169/1125 royal cubits in
point (g). In point (d) the measure 108 8/9 royal cubits was discussed. The quotient of
108 8/9 divided by 11 169/1125 is 9.765625 or 3.125 squared: compare with the preceding
point.
(l) The number 225
The denominator 225 is common in various fractions already discussed: 8 48/225 and
1 195/225, for example. It is productive to divide the height of the Great Pyramid by the
number: 280 royal cubits divided by 225 = 1 55/225 (1.2444 ...) royal cubits which is 25 2/3
inches (royal cubit = 20.625 inches). This new measure has been given the appellation ma'at
by the present writer after the ancient Egyptian goddess Ma'at, wife of the god Thoth.
Intriguing mathematical outcomes can be discovered.
The quotient of 1760 royal cubits (base perimeter of the Great Pyramid) divided by
1 55/225 is 1414.285714 ... (9900/7); the ancient Egyptian fraction for the square root of
two was 99/70: see point (c);
The ma'at of 25 2/3 inches is equivalent to 1.76 remen (cf. common cubit of 17.6 inches
etc.) or 1.458333 ... common cubits: the remen measures 14.58333 ... (14 7/12) inches -
see Figure 2;
Doubling 25 2/3 five times produces 821.333 ... (821 1/3): cf. the volume of the
sarcophagus contents 8.21333 ... (8 48/225) cubic royal cubits discussed in point
(e).
The ma'at of 1 55/225 (1.2444 ...) royal cubits has an interesting relationship with
another commonly-found Greek measure noted by Petrie (MW p. 4). Although he
confusingly refers to it as a Greek foot, it is not the Greek foot of 12 11/72 inches described
earlier: see Figure 5. This alternative Greek foot, he noted, was (about) 12.44 inches. This
is nothing less than the ma'at measure of 25 2/3 inches divided by 2.0625. Furthermore, the
alternative Greek foot - its correct value is 12.444 ... (12 4/9) inches - was 64/75 the remen
measure. The ratio is the same as that between the common cubit of 17.6 inches and the
royal cubit of 20.625 inches.
The alternative Greek foot's most startling connection, though, is with the common cubit:
the quotient of 17.6 inches divided by 12 4/9 inches is 99/70, the square root of two fraction
discussed earlier.
In NADIAE the ma'at measure is shown to be a part of what is one of the greatest design
feats in history.
(m) Khephren's pyramid and the mile
Khephren's pyramid, the second largest of the Egyptian pyramids, exhibits the well-
known 3.4.5 proportions in its design (Petrie, TPTG p. 202). The mean base measure of the
structure is 8474.9 inches (Petrie, TPTG p. 97) or 411 royal cubits (design intention 8476.875
inches). The number 411 is based on the prime numbers 3 and 137. Three is of no interest, it
is too common. The astonishing source of 137 in the design strategy is explicated in
NADIAE. (It should come as no surprise that the geometric configuration described earlier
has a key role in its creation.)
The height of the pyramid was originally 274 royal cubits, the planned volume,
accordingly, was 15,428,118 cubic royal cubits.
Petrie writes of the entrance (TPTG p. 104):
"The doorway of the Second Pyramid is lost, along with its casing; ... The position of the
passage was fixed from a station mark near it; its axis is 490.3 (inches) E. of the middle of
the N. face." (Petrie, 8471.9 inches for the north face, TPTG p. 97)
Note that the north face has a small error of workmanship of about five inches. The
entrance is thus 24 royal cubits (495 inches, design intention) off-centre. Again, the designer
is pointing to something mathematically significant. Take heed of the use of the time number
24 - recall the item on 2.4 remen in point (b) and the 24-digit common cubit discussed in the
Preamble.
If the base measure of 411 royal cubits is divided by 24 the quotient is 17.125 royal
cubits. A cube with such dimensions contains 5022 89/512 cubic royal cubits. A stupendous
design conceptualisation is imminent.
The volume of the pyramid, as stated, is 15,428,118 cubic royal cubits. The quotient of
this number divided by 5022 89/512 is 3072, the number of royal cubits in a mile.
There is evidence of the mile on the ground in Khephren's neighbour, the Great Pyramid;
and of the ancient Egyptians' interest in 3.4.5 proportions; and of the knowledge of latitude
30 degrees North which is two-thirds of the way on a meridian from the North Pole to the
equator.
Charles Piazzi Smyth observed that the Great Pyramid's apex is located around latitude
29 degrees 58 minutes 51 seconds North, give or take a few feet2). It is short of latitude 30
degrees North by around 0.019666 ... degree. The latter is virtually 1 1/3 miles. Now this is
not disputable: a point 1 1/3 miles directly south of latitude 30 degrees North is right inside
the base area of the Great Pyramid close to being under the apex.
(The contemporary polar circumference measure of 24,859.82 miles produces a degree of
around 69.055 ... miles or about 364,610.7 feet; the ancient Egyptian degree was 69.0498 ...
or 69 3160/63,360 miles or 364,583 1/3 feet. The difference is around 27.5 feet. Observe
how the ancient Egyptian degree measure expresses the number of inches in a mile (63,360)
in its make-up; the contemporary degree does not.)
Further astonishing design features can be found in Khephren's Pyramid:
The volume of stone in Khephren's sarcophagus, which Petrie reports as being "well
polished" and "dressed down to the intended height", is easily found by subtracting the
inner contents volume from the overall volume. His measurements in inches
(Petrie,
TPTG p. 107) are shown below on the left, the design intention, which can be deduced
without undue difficulty, on the right. Note the congruency and the links between
numerators and denominators in the design intention.
|
|
Petrie
min. & max. variations
in measurements
|
Mean
|
Design intention
|
|
Outer length:
|
103.62 - 103.73
|
103.68
|
103.7…
|
(2800/27)
|
|
Outer width:
|
41.95 - 42.0
|
41.97
|
41.96 …
|
(1133/27)
|
|
Outer height:
|
37.98 - 38.12
|
38.12
|
38.12 ...
|
(43,200/1133)
|
|
Inner length:
|
84.63 - 84.91
|
84.73
|
84.72 …
|
(7,246,711/85,536)
|
|
Inner width:
|
26.66 - 26.76
|
26.69
|
26.69 …
|
(2376/89)
|
|
Inner depth:
|
29.51 - 29.68
|
29.59
|
29.666 ...
|
(89/3)
|
The volume of 11.264 cubic royal cubits (0.22 doubled nine times), or 98,826.75 cubic
inches, is the volume of the King's Chamber sarcophagus contents of 8 48/225 cubic royal
cubits multiplied by 48/35; a remen digit is 35/48 (0.7291666 ...) inch. Recall the stade
measure of 7291 2/3 (7291.666 ... ) inches described in point (h)
and BU in Figure 3.
The volume of Khephren's tomb-chamber is 2800 cubic royal cubits which is
24,566,308 304/512 cubic inches (readily deduced from Petrie's measurements shown on
pp. 105 - 6 of TPTG). The chamber has a gabled roof.
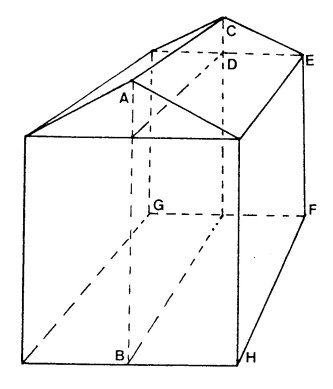 General layout of Khephren's tomb-chamber
General layout of Khephren's tomb-chamber
The Petrie/Vyse mean dimensions are shown below on the left, the design intention on
the right:
|
|
|
Petrie/Vyse
inches
|
Design intention inches
|
as royal cubits
|
|
End height:
|
AB
|
244.4
|
244 29/684 (244.04)
|
11 427/513
|
|
Roof height:
|
CD
|
38
|
37 271/342 (37.79)
|
1 427/513
|
|
Wall height:
|
EF
|
206.4
|
206.25
|
10
|
|
Breadth:
|
GF
|
195.9
|
195.9375
|
9.5
|
|
Length:
|
FH
|
557.4
|
556.875
|
27
|
The volume of the chamber (design intention) from the floor to the top of the wall is 2565
cubic royal cubits (22,504,493 209/512 cubic inches), the gabled roof space 235 cubic royal
cubits (2,061,815 5/27 cubic inches).
Outcomes
The quotient of the tomb-chamber volume 2800 cubic royal cubits divided by 11.264, the
volume of stone in the sarcophagus, is 248.5795454 ... (248 102/176). This is a clear
reference to the ancient Egyptian measure of the world 24,857.95454 ... (70,000,000/2816)
miles which is equivalent to, as reported in point (h), 216,000 (60 cubed) stades.
The renowned historical figure Eratosthenes said the circumference of the earth was
252,000 stades (Morgan, p. 27). He faked the real measure by adding 36,000 stades (cf. 360
degrees in a circle, 360 days in an ancient Egyptian year) to fool enemies or those not
initiated into the Greco/Egyptian Mysteries. Vitruvius, proven in NADIAE to be an initiate
into these Mysteries, makes a telling comment on the matter in De Architectura:
"Some people do indeed say that Eratosthenes could not have inferred the true measure of the
earth." (Morgan, p. 28)
The linear measure of 11.264 royal cubits affords the opportunity of finding a series of
interlocking relationships: 11.264 royal cubits is 232.32 inches or 19.36 feet; 19.36 is 4.4
squared; 4.4 feet is 52.8 inches; a mile is 5280 feet; the quotient of 1760 royal cubits
(perimeter of the Great Pyramid base) divided by 11.264 is 156.25 which is 12.5 squared;
12.5 royal cubits is 257.8125 inches or 14.6484375 common cubits or 351.5625 common
cubit digits; 351.5625 is 18.75 squared.
If 351.5625 common cubit digits were the measure of a diagonal in a square and the
fraction 99/70 were taken to represent the square root of two, that square's sides would
measure 248.5795454 ... (248 102/176) common cubit digits: refer to the Khephren
tomb-chamber material in Outcomes above, the measure of the world again, and compare 351.5625
with the Atlantis material in point (h).
NEXT
VisMath Home