|
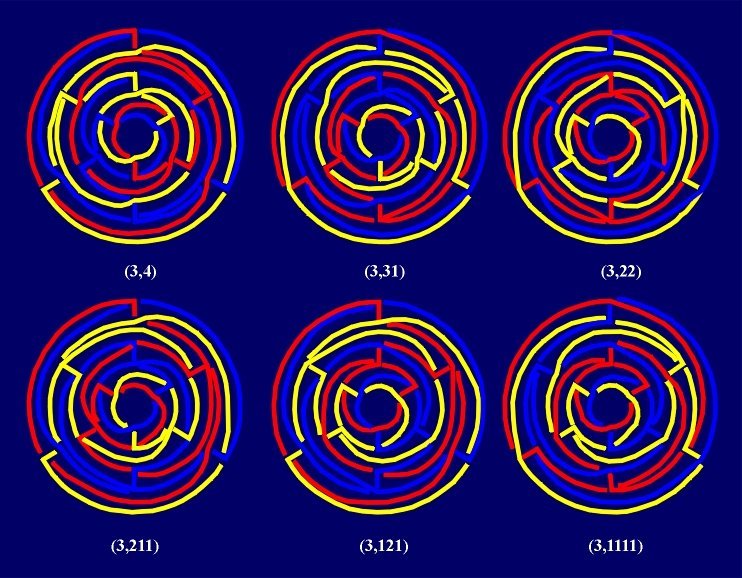
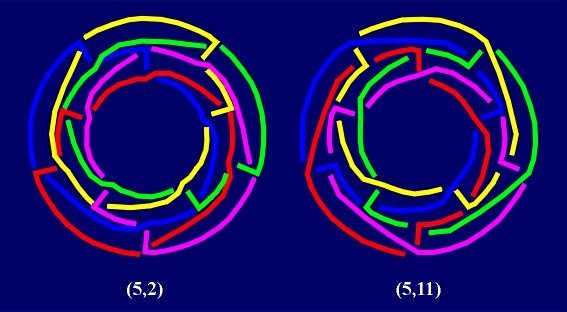
"Prismatic" Borromean links
Tessellations of (2n+1)-gonal prism, where in every ring of the projection
we draw "left" or "right" diagonals, yield the next infinite
series. The notation of the tessellations and links can be done using the symbols
(2n+1, k), where all decompositions of the number
k=(2n+1)l-2, are denoted by k,
such that every decomposition is identified with its obverse. From each such
tessellation with k rings we obtain
2k-2+2[k/2]-1 different
(2n+1)-Borromean links without the Brunnian property.
In those links, all components are equivalent, i.e. there is an
isotopy of 3-space that carries the link to itself and any given
component onto any other. Then the digons could be introduced again,
in the same way as before.
|

|
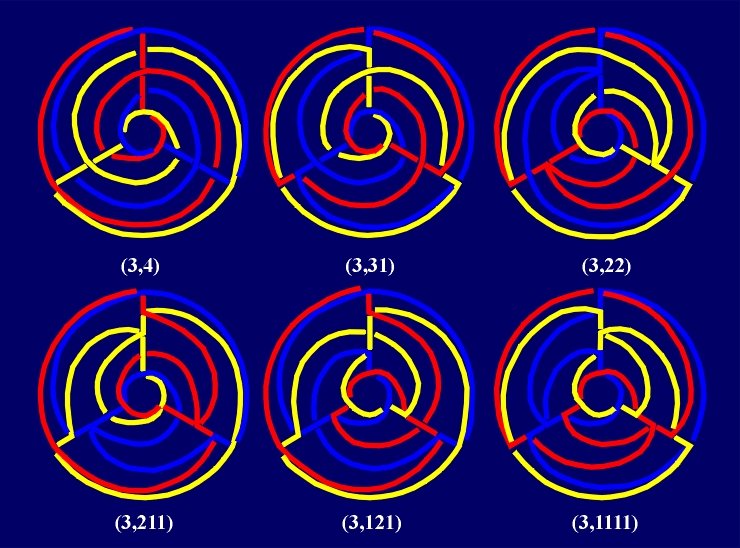
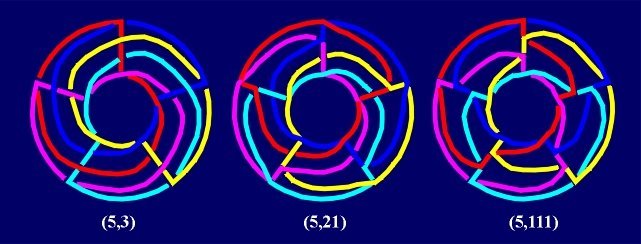
The same method, using "centered" rectangular tessellations, provides another series of (2n+1)-Borromean links. |